来聊聊HashMap底层红黑树
什么是红黑树
在权威书籍中,对于红黑树的解释是这样的:
- 每个节点或者红色,或者是黑色。
- 根节点为黑色。
- 每一个叶子节点都是黑色。
- 如果一个节点是红色,那么他的孩子节点都是黑色。
- 从任意一个节点,经过的黑色节点是一样的。
在《算法4》一书中认为红黑树和2-3树木是等价的。
2-3树简介
2-3数的2节点和3节点
在了解2-3树之前,我们必须了解2-3树节点:
- 满足二分搜索树的基本性质。
(左节点小于节点,右节点大于节点) - 节点分为2节点和3节点,2节点即可以挂两个子节点。3节点即可挂3节点。
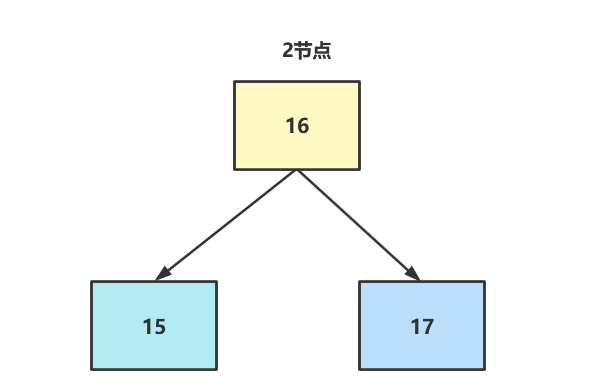
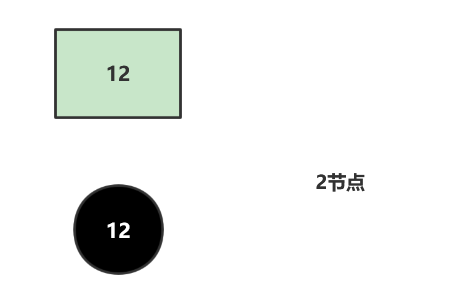
如下图所示,这就是典型的2-3树的2节点,可以看到2节点即父节点存放一个元素的节点,这种节点只能挂两个元素。
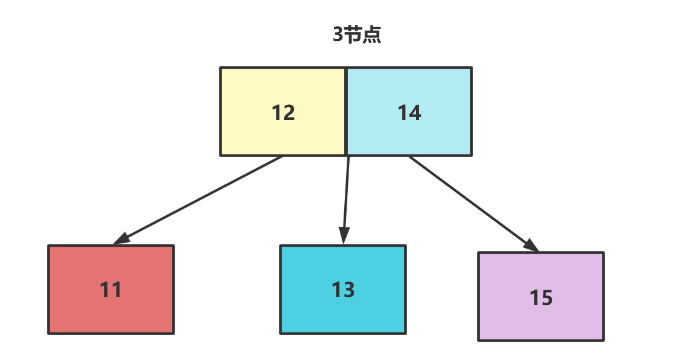
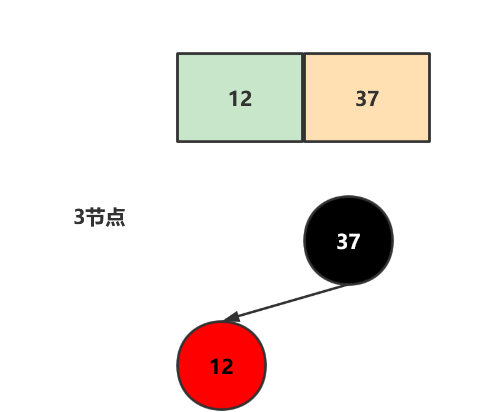
3节点如下图所示,可以看到父节点下挂着3个节点。
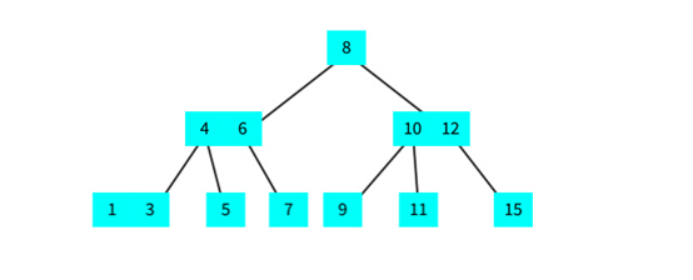
红黑树的整体结构如下图所示
#2-3树是绝对平衡树
绝对平衡树的定义即任何时刻任意节点,左节点和右节点的层数都是一样的。那么2-3树是如何实现绝对平衡的呢?
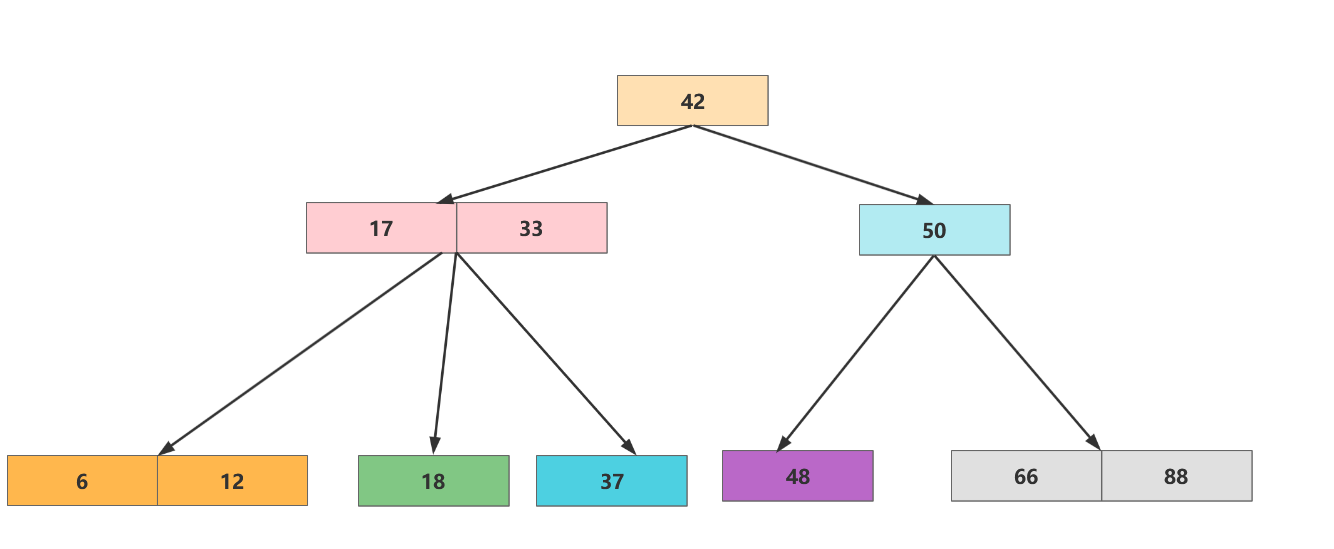
假设我们要将下面的节点存放到2-3树中:
42 37 12 18 6 11 5首先添加42,由于2-3树为空,所以直接插入即可。
然后再插入37 ,如下图所示,37比42小,所以理应插入到42的左节点中,但是左节点为空,所以他只能作为42的邻节点,由此构成一个3节点。
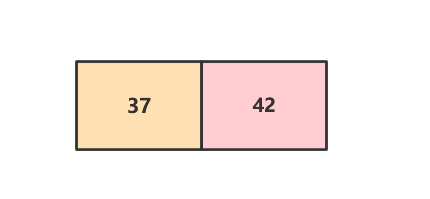
插入12,此时构成了一个4节点,不符合2-3树节点的特征,所以需要将节点拆解。如下图所示
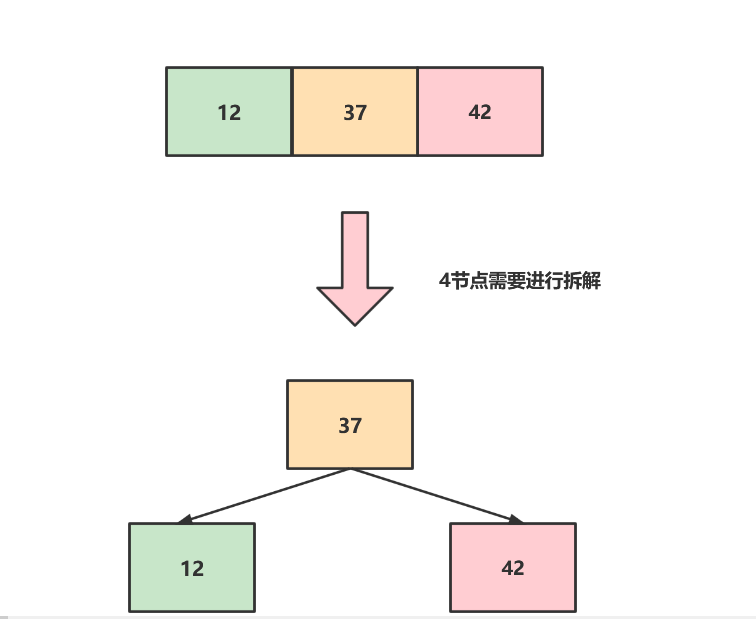
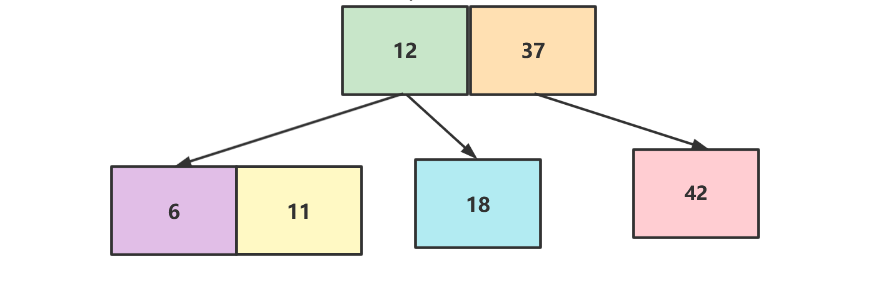
在添加18,比37小,比12大,所以要插入到12的右子节点,但是右子节点为空,所以18就和12合并变为3节点
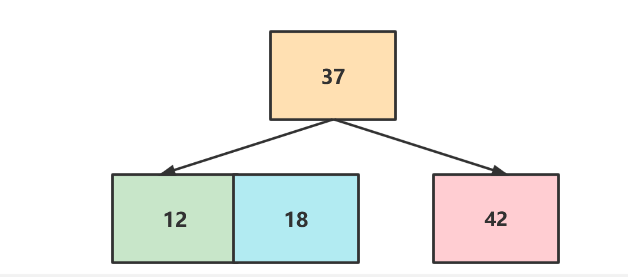
再添加6,构成一个4节点需要拆解,导致失衡,所以拆解后的父节点要向上融合,如下图
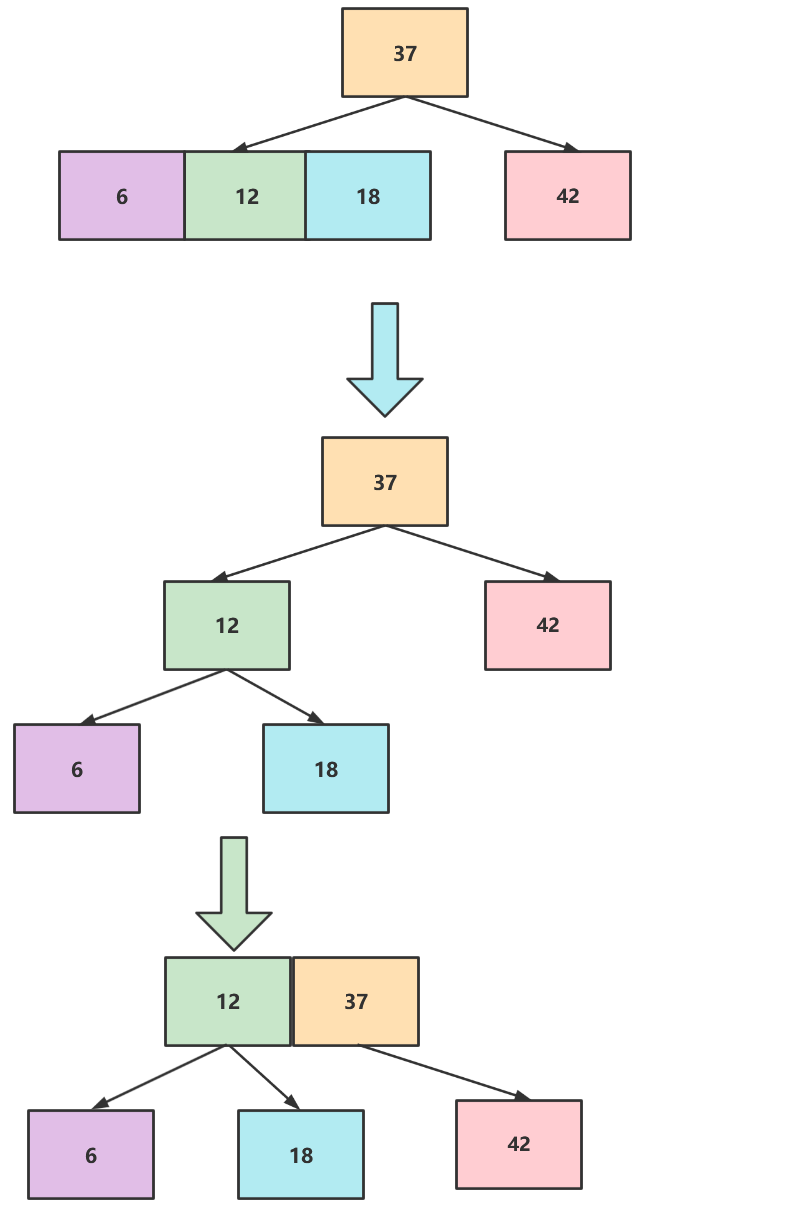
再添加11,同理挂到6的右边。
最后添加3,构成1个4节点,拆解后再向上融合,有构成一个4树,再次拆解,如下图
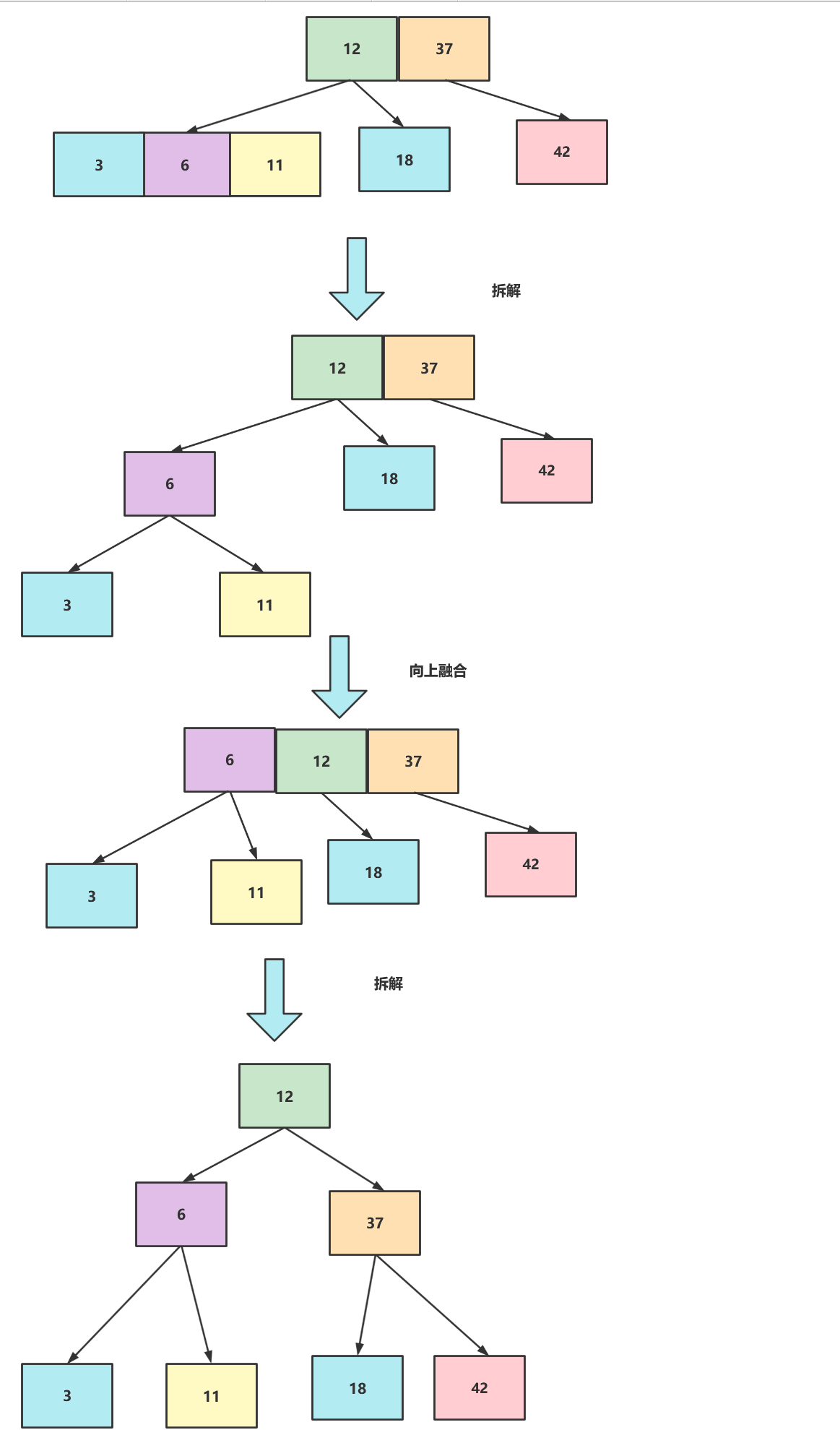
可以看到笔者从42开始添加的节点都小于42,若按照二分搜索树的添加逻辑,很可能会退化成链表。而2-3树在任何时候都能够保持平衡,所以我们说2-3树是一个绝对平衡树。
红黑树
红黑树和2-3树的关系
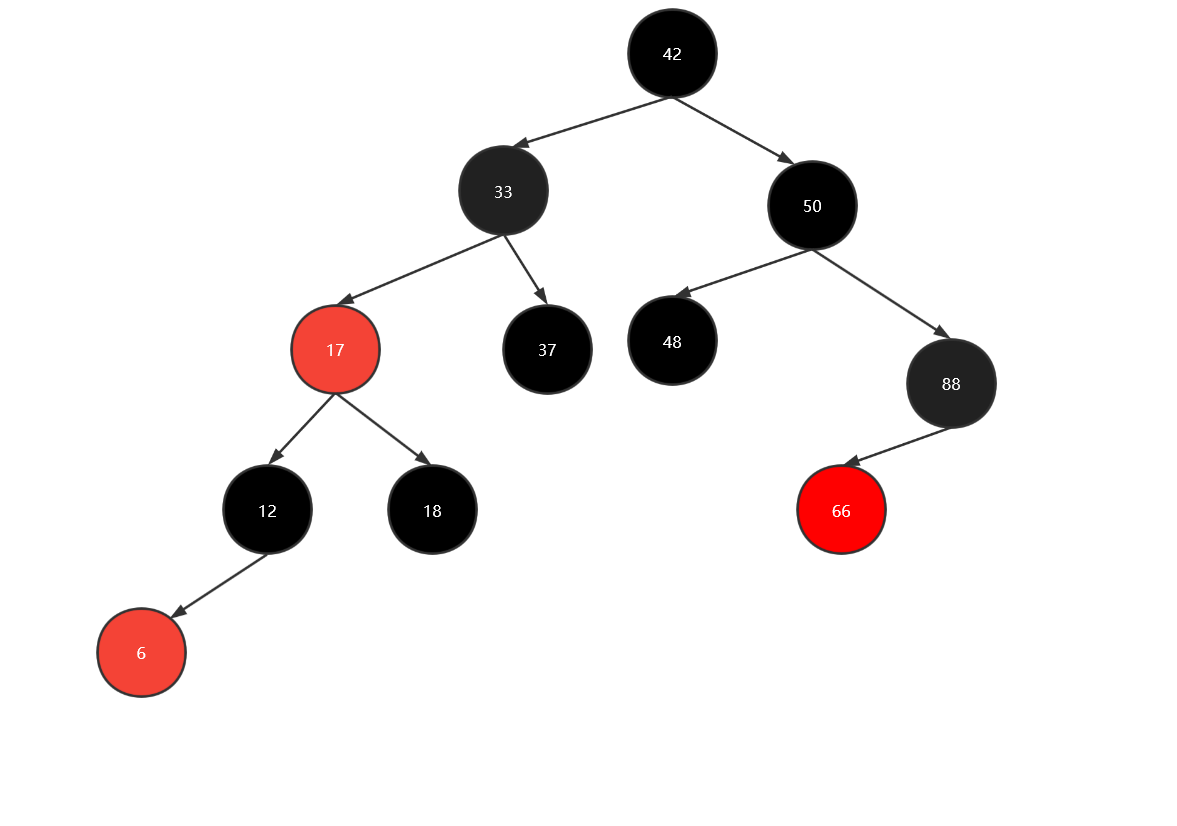
上文已经提到了红黑树和2-3树是等价的,我们完全可以将2节点当作红黑树的黑节点,而3节点当作红黑树的红黑节点,如下图所示:
如下图所示,根据上面描述我们给出这样一颗2-3树,将其转为红黑树后就如图2所示:
可以转为红黑树只需将2-3树的3节点的左节点染红,例如上图的6、12组成的3节点,我们只需将6染红,作为黑节点12的左节点即可。
红黑树的特点
- 从任意节点到另外一个叶子节点,经过的黑节点是一样的。
- 严格意义上,红黑树是一个绝对的
“黑平衡树”,即我们将红节点和其父节点当作一个整体,我们就会发现,这个红黑树的层级是绝对平衡的。而将"将红节点和其父节(黑节点)点当作一个整体"的过程,就是2-3树。
红黑树复杂度
最大高度为2N(logN),所以添加复杂度估算为O(logN)
红黑树如何添加元素
添加一个比插入位置大的节点
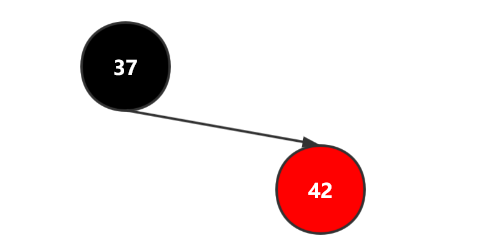
以2-3数为例,假设我们树中只有一个节点37,此时插入一个42,按照2-3树的做法,会将42插入到37的右子节点,但此时2-3数还没有右子节点,所以就将其添加到自己的右边,又称3节点。
若是红黑树,则是这样,很明显这违背了红黑树的特征,所有的红节点都必须位于左节点。所以我们需要对其进行翻转
如同下图所示,我们对其进行了一次左旋,并将右边染黑,左边染红。
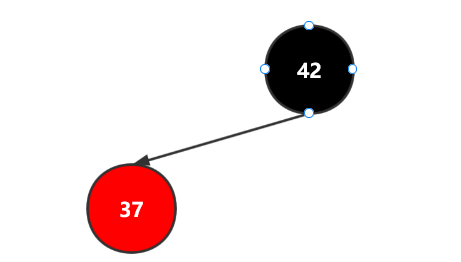
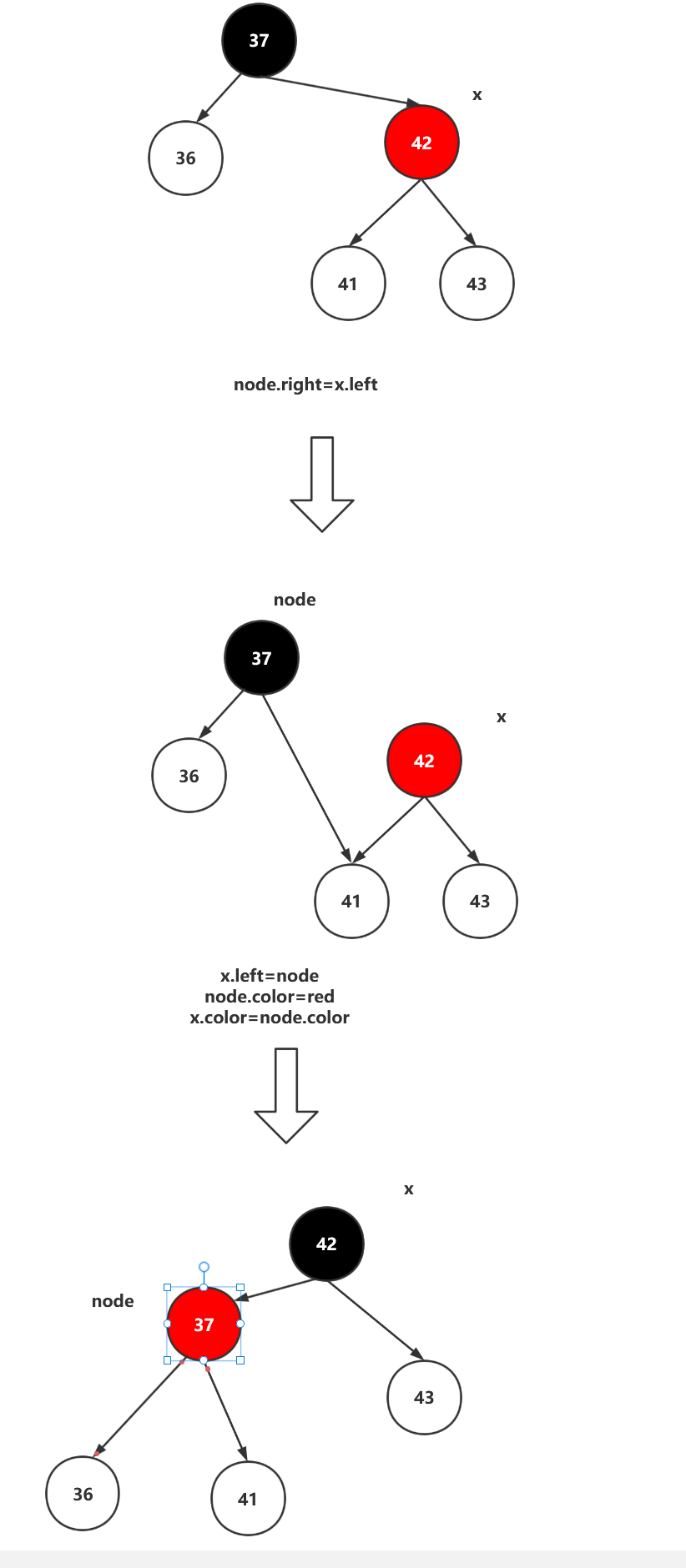
假设我们已经完成了一次插入,此时42是红的显然不合逻辑(从黑平衡角度来看,37左边有1层,42为2层,是失衡的),所以我们需要进行一次左旋转。 见下图,因为红黑树也是有序树,所以42下的所有节点都大于37,所有将42下最小的节点挪到37的右边,再让42指向27即可构成黑平衡,见下图。
完整的代码如下
/**
* 插入的节点构成3节点,但是红节点在左边,需要进行左旋
*
* @param node
* @return
*/
private Node leftRotate(Node node) {
// 找到node节点的左节点
Node x = node.right;
//左旋
node.right = x.left;
x.left = node;
//颜色翻转
x.color = node.color;
node.color = RED;
return x;
}连续添加两个节点都在左边
如下图,构成了一个左倾斜的节点,导致失衡。
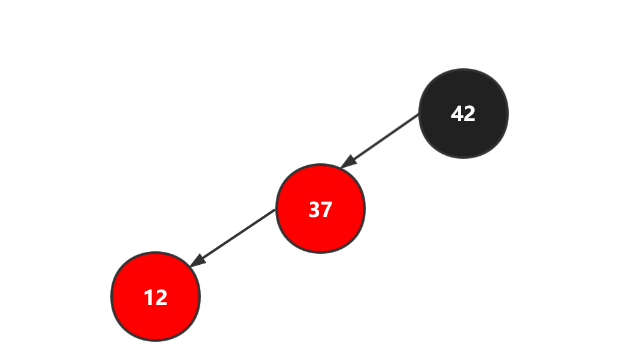
对此我们就需要进行一个右旋的操作,如下图,因为红黑树的有序性,这使得42这个根节点大于左边的所有节点,所以我们将左节点中最大的节点作为42的左节点,让37作为根节点,完成黑平衡,如下图。
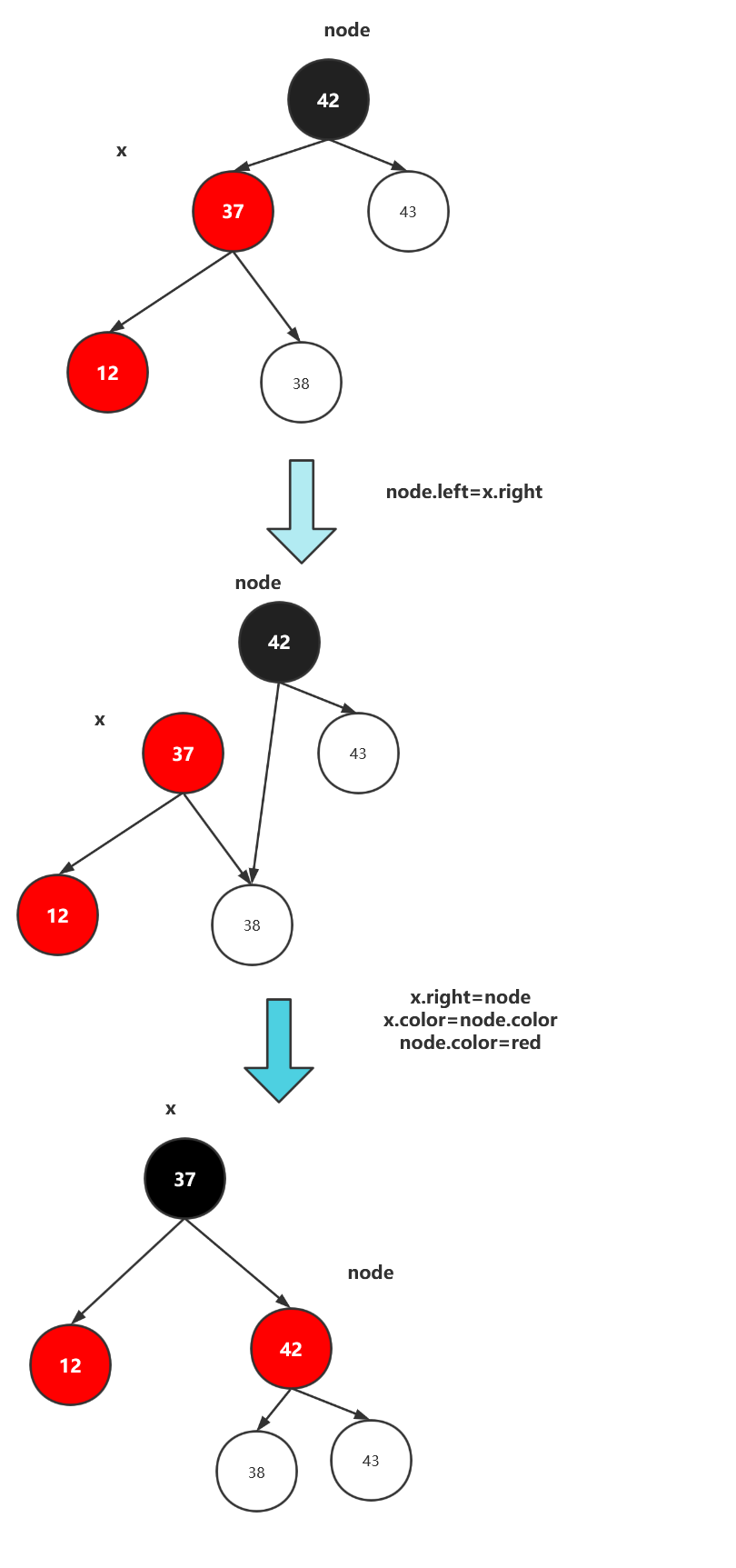
可以看到虽然完成了右旋转的操作,但是最终的左右节点都是红的,导致红黑树并不是黑平衡的,所以这里就需要一次颜色翻转。这里我们先贴出右旋转的代码,在介绍颜色翻转逻辑
private Node rightRotate(Node node) {
Node x = node.left;
node.left = x.right;
x.right = node;
node.color = RED;
x.color = node.color;
return x;
}添加节点后子节点都变红
在上文右旋操作导致,颜色错误进而出现红黑树违背黑平衡的情况,所以我们需要进行颜色翻转,如下图,我们将子节点都为红的节点染黑,再将父节点染红(父节点会将笔者后续的递归逻辑中变黑)。
这样依赖37左节点层级为1,右节点层级也为1(黑平衡要求我们将左红节点和黑节点看作一个整体)
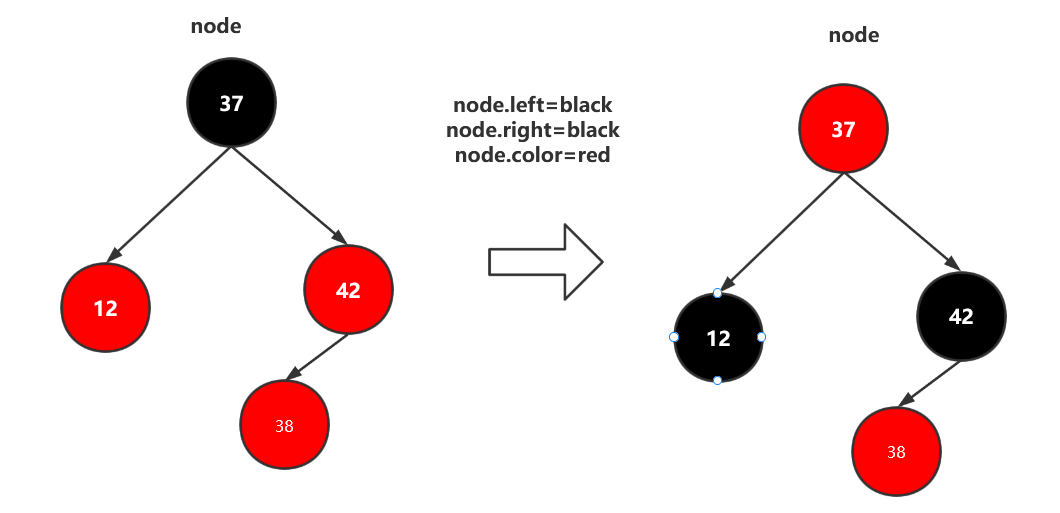
添加节点成为LR型
如下图,LR型就是37 12 13这样的插入顺序,对此我们只需左旋再右旋最后颜色翻转一下即可
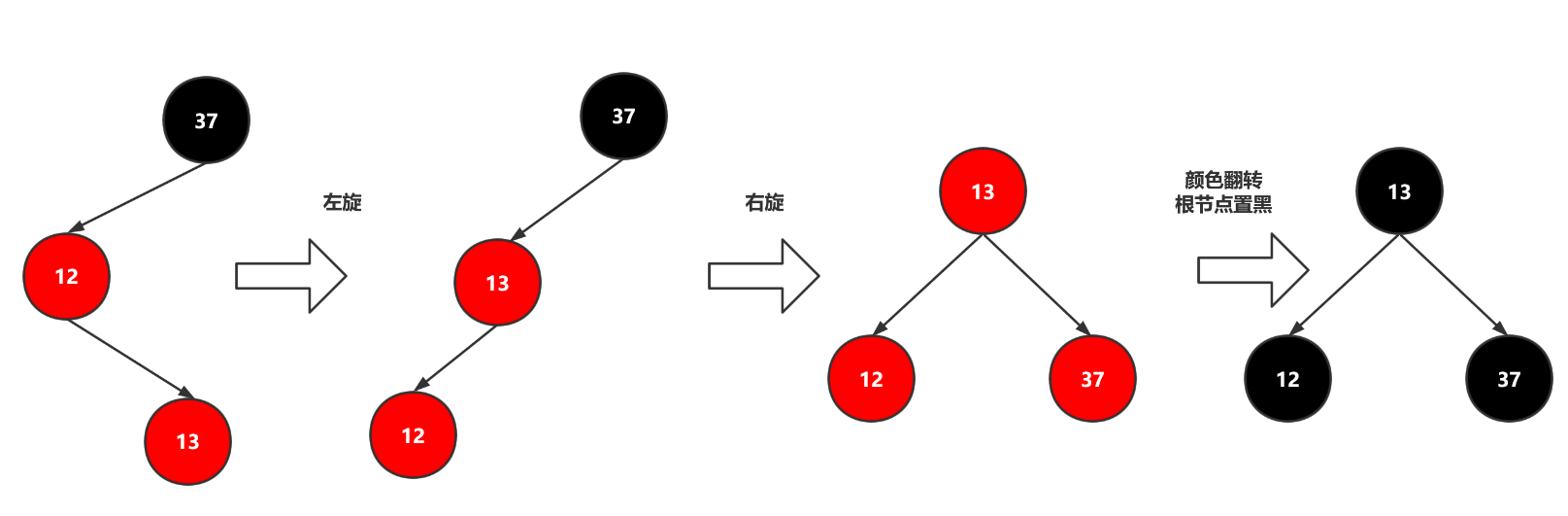
手写红黑树
节点描述
我们都知道红黑树是由红黑两种节点构成,所以我们需要声明颜色的变量。
红黑树是由一个个节点构成,所以我们需要声明节点内部类,内该内部类拥有颜色、左节点、右节点、key、val几个属性。
有了节点内部类,我们就需要对红黑树类添加相关属性描述了,首先是红黑树的容量、其次红黑树的操作都需要从树根开始,所以我们需要首节点root、以及容量size。
红黑树插入都需要和每个key进行比较,所以红黑树类的k要求可以比较,所以我们定义的红黑树要求是泛型类,并且泛型key必须是可比较的,所以这个k泛型需要继承Comparable。
完成这些铺垫之后,我们就需要进行插入操作的逻辑分析了,我们不妨对上文长篇论述的插入过程进行整理一下:
1. 插入的节点在当前节点右边,导致红节点在右边,需要进行左旋转保证黑平衡。 2. 连续插入两个节点都在当前节点左边,导致向左倾斜,需要进行右旋转保持平衡。 3. 第一次插入的节点在当前节点左边,然后再插入一个节点在红黑树右边导致红黑树失衡。我们需要先左旋一下,再右旋一下。 4. 当前节点的左节点和右节点都是红色的,需要将颜色翻转为黑色。分析之后我们发现3这个一点包含了1、2的操作,所以我们编写3、4两个点的逻辑就可以实现上面的所有功能了,如下图:
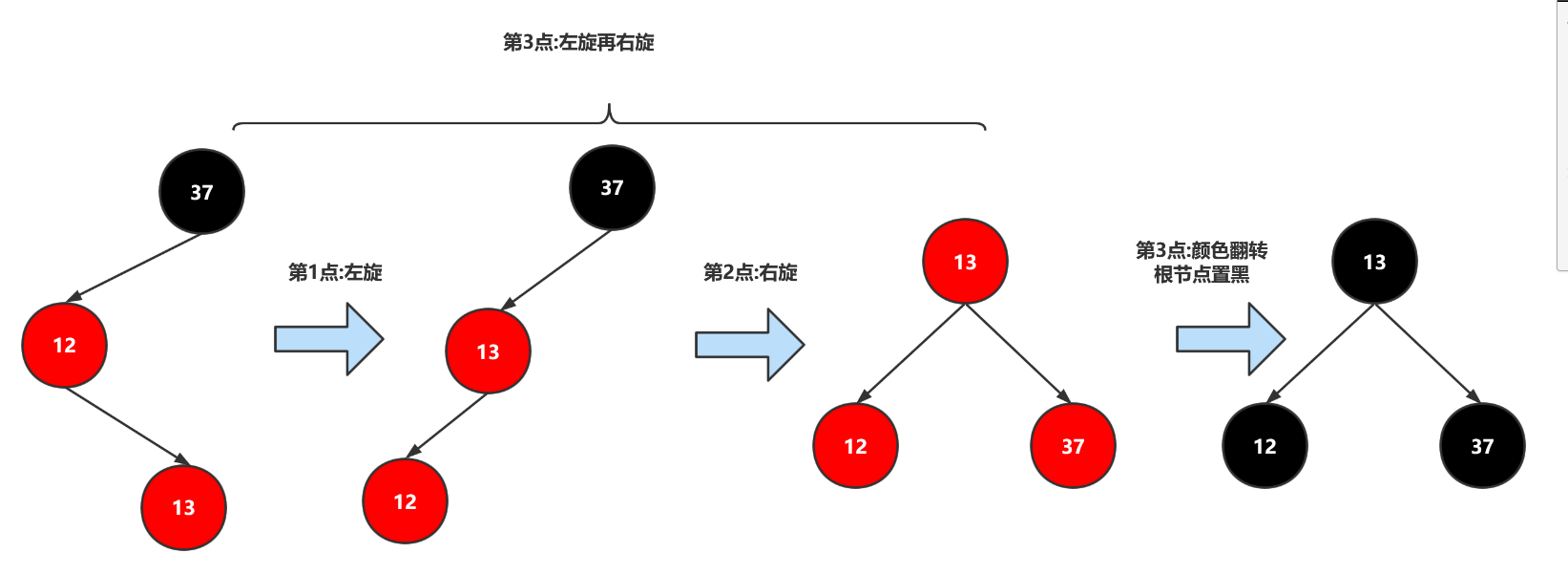
- 注意红黑树要求根节点为黑色,所以我们完成上述的操作之后,需要手动将根节点变为黑色。
对核心逻辑完成梳理之后,我们就可以开始对红黑树展开编码了。
创建红黑树类
可以看到我们声明的k泛型继承Comparable
public class RedBlackTree<K extends Comparable<K>, V>节点颜色常量声明
private static final boolean RED = true;
private static final boolean BLACK = false;节点内部类
private class Node < K, V >
{
private K key;
private V val;
private Node left, right;
private boolean color;
public Node(K key, V val)
{
this.key = key;
this.val = val;
this.left = null;
this.right = null;
this.color = RED;
}
}红黑树容量、首节点、构造方法声明
private Node root;
private int size;可以看到构造方法初始化了首节点为空,容量为0
public RedBlackTree(){
this.root = null;
this.size = 0;
}实现节点添加逻辑
首选是左旋的逻辑,这一点我们在上文图解添加过程时已经写好了伪代码,补充完成即可。
/**
* 插入的节点构成3节点,但是红节点在左边,需要进行左旋
*
* @param node
* @return
*/
private Node leftRotate(Node node) {
// 找到node节点的左节点
Node x = node.right;
//左旋
node.right = x.left;
x.left = node;
//颜色翻转
x.color = node.color;
node.color = RED;
return x;
}右旋逻辑
private Node rightRotate(Node node) {
Node x = node.left;
node.left = x.right;
x.right = node;
node.color = RED;
x.color = node.color;
return x;
}颜色翻转
private void flipColors(Node node) {
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}完成后我们就可以根据上文分析的添加逻辑,编写3、4逻辑整合
首先为了代码复用,我们编写一下颜色判断的逻辑,注意若节点不存在,我们也认定这个节点为黑
private boolean isRed(Node < K, V > node) {
if(node == null) {
return false;
}
return node.color == RED;
}然后完成添加逻辑,可以看到笔者通过递归将3、4逻辑完成的红黑树的添加操作,完成添加操作并旋转平衡后的当前节点。
private Node < K, V > add(Node < K, V > node, K key, V val) {
if(node == null) {
size++;
return new Node(key, val);
}
if(key.compareTo(node.key) < 0) {
node.left = add(node.left, key, val);
} else if(key.compareTo(node.key) > 0) {
node.right = add(node.right, key, val);
} else {
node.val = val;
}
// 左节点不为红,右节点为红,左旋
if(isRed(node.right) && !isRed(node.left)) {
node = leftRotate(node);
}
// 左链右旋
if(isRed(node.left) && isRed(node.left.left)) {
node = rightRotate(node);
}
// 颜色翻转
if(isRed(node.left) && isRed(node.right)) {
flipColors(node);
}
return node;
}完成核心逻辑后,我们就将根节点变黑即可,考虑封装性,我们将上文方法封装成一个add允许外部传键值进来。
public void add(K key, V val) {
root = add(root, key, val);
root.color = BLACK;
}补充剩余逻辑
获取容量和获取根节点
public int getSize() {
return size;
}
private Node getRoot() {
return root;
}用层次遍历法测试结果
我们希望测试红黑树添加的准确性,所以我们用尝试用代码添加以下几个节点
150 172 194 271 293 370完成后的树应该如下图所示
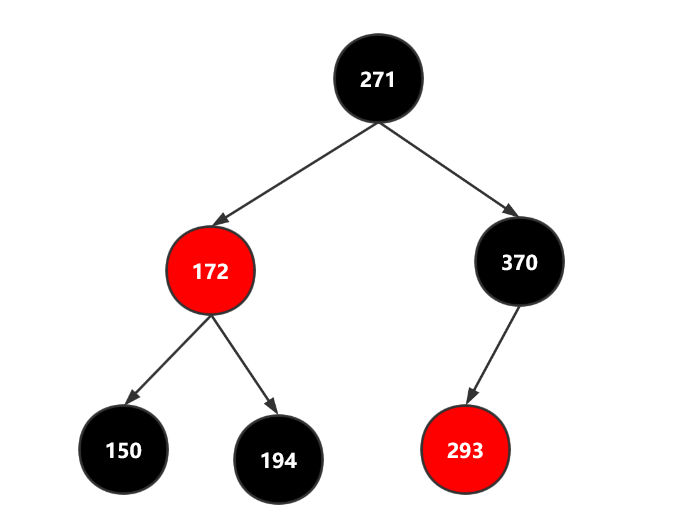
为了验证笔者代码的准确性,我们编写一段层次遍历的测试代码,按层次顺序以及颜色输出节点
public void levelOrder() {
Node root = this.getRoot();
ArrayDeque < Node > queue = new ArrayDeque();
queue.add(root);
while(!queue.isEmpty()) {
Node node = queue.pop();
System.out.println("key:" + node.key + " val: " + node.val + " color:" + (node.color == RED ? "red" : "black"));
if(node.left != null) {
queue.add(node.left);
}
if(node.right != null) {
queue.add(node.right);
}
}
}测试代码,可以看到输出结果正确
public static void main(String[] args) {
RedBlackTree < Integer, String > rbTree = new RedBlackTree < > ();
rbTree.add(150, "");
rbTree.add(172, "");
rbTree.add(194, "");
rbTree.add(271, "");
rbTree.add(293, "");
rbTree.add(370, "");
rbTree.levelOrder();
/**
* 输出结果
*
* key:271 val: color:black
* key:172 val: color:red
* key:370 val: color:black
* key:150 val: color:black
* key:194 val: color:black
* key:293 val: color:red
*/
}Java中HashMap关于红黑树的使用
插入
我们都知道Java中的HashMap在底层数组容量为64且当前这个通元素达到8时会触发扩容,对此我们不妨写一段代码测试一下,代码如下所示,可以看到笔者为了更好的演示,将每一个map的value值声明为当前key在hashMap底层数组中的索引位置。所以我们在map.put("590", "Idx:12");打上断点
HashMap < String, String > map = new HashMap < String, String > (64);
map.put("24", "Idx:2");
map.put("46", "Idx:2");
map.put("68", "Idx:2");
map.put("29", "Idx:7");
map.put("150", "Idx:12");
map.put("172", "Idx:12");
map.put("194", "Idx:12");
map.put("271", "Idx:12");
map.put("293", "Idx:12");
map.put("370", "Idx:12");
map.put("392", "Idx:12");
map.put("491", "Idx:12");
//转红黑树
map.put("590", "Idx:12");核心代码如下所示,我们传入的590的key会在i为12的链表中不断查找空闲的位置,然后完成插入,循环过程中会记录当前链表元素个数binCount ,经过判断binCount >TREEIFY_THRESHOLD - 1即8-1=7,然后调用treeifyBin看看是扩容还是转红黑树
final V putVal(int hash, K key, V value, boolean onlyIfAbsent, boolean evict) {
Node < K, V > [] tab;
Node < K, V > p;
int n, i;
if((tab = table) == null || (n = tab.length) == 0) n = (tab = resize()).length;
//计算出hashMap这个key对应索引Ii的位置
if((p = tab[i = (n - 1) & hash]) == null) tab[i] = newNode(hash, key, value, null);
else {....略
//核心逻辑在这里,我们传入的590的key会在i为12的链表中不断查找空闲的位置,然后完成插入,循环过程中会记录当前链表元素个数binCount ,经过判断binCount >TREEIFY_THRESHOLD - 1即8-1=7,然后调用treeifyBin转红黑树
for(int binCount = 0;; ++binCount) {
if((e = p.next) == null) {
p.next = newNode(hash, key, value, null);
if(binCount >= TREEIFY_THRESHOLD - 1) treeifyBin(tab, hash);
break;
}
//.....
}
}
//.........略
}我们再来看看treeifyBin,可以看到如果数组容量小于64直接扩容,反之就是将当前节点转为树节点然后调用treeify转红黑树,关于红黑树的逻辑上文已经详细说明了这里就不多赘述了。
final void treeifyBin(Node < K, V > [] tab, int hash) {
int n, index;
Node < K, V > e;
//如果数组容量小于64直接扩容
if(tab == null || (n = tab.length) < MIN_TREEIFY_CAPACITY) resize();
else if((e = tab[index = (n - 1) & hash]) != null) {
TreeNode < K, V > hd = null, tl = null;
do {
//将节点转为树节点,hd即为head指向当前链表头节点,然后后续节点一次转为树节点和前驱节点彼此指向,从而构成一个双向链表
TreeNode < K, V > p = replacementTreeNode(e, null);
if(tl == null) hd = p;
else {
p.prev = tl;
tl.next = p;
}
tl = p;
} while ((e = e.next) != null);
//如果hd不为空说明需要转红黑树,调用treeify
if((tab[index] = hd) != null) hd.treeify(tab);
}
}HashMap中的红黑树是如何完成查询的呢?(重点)
HashMap源码如下,首先通过hashCode找到桶的位置,然后判断这个桶是否只有一个元素,如果没有则直接返回,反之调用getTreeNode从红黑树中找到对应的元素
final Node < K, V > getNode(int hash, Object key) {
Node < K, V > [] tab;
Node < K, V > first, e;
int n;
K k;
if((tab = table) != null && (n = tab.length) > 0 &&
//计算hash对应的节点first
(first = tab[(n - 1) & hash]) != null) {
//如果有且只有一个则直接返回
if(first.hash == hash && ((k = first.key) == key || (key != null && key.equals(k)))) return first;
if((e = first.next) != null) {
//如果是红黑树则调用getTreeNode
if(first instanceof TreeNode) return((TreeNode < K, V > ) first).getTreeNode(hash, key);
do {
if(e.hash == hash && ((k = e.key) == key || (key != null && key.equals(k)))) return e;
} while ((e = e.next) != null);
}
}
return null;
}我们步入getTreeNode会看到find方法,可以看到它查询红黑树的元素逻辑很简单,根据红黑树的有序性找到和查询元素hash值相同、equals为true的节点返回即可。
final TreeNode < K, V > find(int h, Object k, Class <? > kc) {
TreeNode < K, V > p = this;
do {
int ph, dir;
K pk;
TreeNode < K, V > pl = p.left, pr = p.right, q;
//比对元素hash值大于h,p指向p的左子节点进行下一次比对
if((ph = p.hash) > h) p = pl;
//比对值小于查询节点的hash,p指向右子节点进行下一次比对
else if(ph < h) p = pr;
//如果key一样且equals为true直接返回这个元素
else if((pk = p.key) == k || (k != null && k.equals(pk))) return p;
else if(pl == null) p = pr;
else if(pr == null) p = pl;
else if((kc != null || (kc = comparableClassFor(k)) != null) && (dir = compareComparables(kc, k, pk)) != 0) p = (dir < 0) ? pl : pr;
else if((q = pr.find(h, k, kc)) != null) return q;
else p = pl;
} while (p != null);
return null;
}更多关于红黑树
这里仅仅介绍了红黑树的添加逻辑,更多关于红黑树的操作逻辑可以参考这个仓库
可以看到红黑树的逻辑起始并没有那么复杂,只要读者专注核心概念,用一些简单的示例画图了解过程,再通过需求分析所有逻辑和设计之后,编码就没有那么困难了。 既使遇到问题,我们也可以抓住数据结构的特点,配合使用debug+中序遍历也能解决逻辑漏洞。从而加深对数据结构的理解。
二分搜索树、AVL树、红黑树三者使用场景
随机添加节点
若节点存在大量随机性,使用二分搜索树即可,相比于红黑树的2O(nLogN)复杂度,二分搜索树的O(logN)性能更佳,但是二分搜索树可能存在退化成链表的情况,需谨慎考虑。
仅作查询
对于查询AVL最合适不过。他的平衡高度为logn比红黑树的“黑平衡”那种2logn的平衡要出色很多,在添加少,查询多的情况下,使用AVL树更合适。
综合操作
若需要增删改查等综合操作,建议使用红黑树,红黑树虽然不是最优但是综合上是最优的。
参考文献
HashMap源码(JDK1.8)深度分析-红黑树(插入)(opens new window)
[面经手册 · 第4篇《HashMap数据插入、查找、删除、遍历,源码分析》](https://bugstack.cn/md/java/interview/2020-08-13-面经手册 · 第4篇《HashMap数据插入、查找、删除、遍历,源码分析》.html#_1-插入)
 XfyCoding博客
XfyCoding博客